Érdekszférák találkozása

Kiegyenlítenek a golyók: most már ők is el tudják találni szegény játékost. Nagy baj egyelőre nem történik: a játékos némi nyávogás kiséretében a pálya közepén találja magát újra.

Sajnos az ütközés koncepcióját újra kellett gondolnom. Az előző változathoz bőven elég volt az, hogy a szigonyt és a golyókat is a befoglaló téglalapjukkal közelítettem. Ez azonban a játékoz eltalálásához nem elég pontos, mert egy csomószor találatot jelez, amikor valójában a játékost golyónak csak a befoglaló téglalap csücske éri el.

Az, hogy képpontonként ellenőrizzem a találatot, sajnos igencsak időigényes lenne, lévén a PC-k hardwere (szemben a játékmasinákkal és régi Commodore 64-ekkel) ezt a műveletet nem támogatja.

Marad a matematikai módszer. Szerencsére az oskolában felkészítettek ilyen, és ehhez hasonló problémák kezelésére. A módszer, amivel az ellenőrzést végzem, a következő:

1. Először is, elvégzem a befoglaló téglalapos ellenőrzést, mert az gyors, és általában eredményes, mivel többször nincs találat, mint ahányszor van. Ha ez nem vezet negatív eredményre, akkor végzem csak el egy kőr és egy téglalap találatának (számításigényesebb) ellenőrzését.
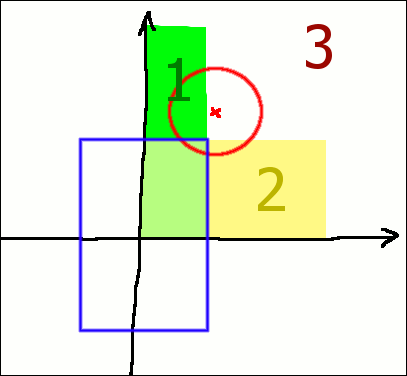
2. Először is, fogom a téglalap és a kőr koordinátáit, és eltolom úgy, hogy a téglalap közepe legyen az origóban. Innentől, mivel a helyzet az origóra szabályos, a kőr középpontjának koordinátáinak az abszolút értékeivel dolgozom, máris jóval egyszerűbb a dolgom.
3. Ha a kőr középpontjának X koordinátája közelebb van az origóhoz, mint a téglalap X irányú élhosszának fele, akkor megnézem, hogy a kőr sugara eléri-e a téglalap határát. Ha igen, van találat, ha nem, nincs.
4. Ugyanezt elvégzem Y irányban. (Ez a második eset)
5. A fennmaradó harmadik az az eset, amikor a kőr középpontja a téglalap jobb-felső sarkától jobbra-felfelé esik. Ilyenkor azt kell megnézni, hogy a kőr középpontjának a távolsága a téglalap jobb-felső sarkától messzebb vagy közelebb van-e, mint a kőr sugara. Ehhez a Pitagorasz-tétel jól használható.

• Vannak hangok is: Lövés upload:upipang4/shoot.voc, találat upload:upipang4/pop.voc, elhalálozás upload:upipang4/meow.voc . A hangokhoz kicsit el kellett molyolni az SDL::Mixer osztállyal, aminek a dokumentáltsága, khm, közepes.

A program szokásosmód megtalálható itt: upload:upipang4/upipang.txt